Mathematical puzzles are engaging brain teasers that combine logical reasoning with numerical challenges. They offer a fun way to explore mathematical concepts while enhancing problem-solving skills and creativity.
1.1 What Are Mathematical Puzzles?
Mathematical puzzles are intellectual exercises that combine logical reasoning with numerical or geometric challenges. They are designed to stimulate problem-solving skills and creative thinking. These puzzles often involve patterns, sequences, or spatial relationships, requiring participants to apply mathematical concepts in innovative ways. Unlike traditional math problems, puzzles typically present an engaging and fun experience, making them accessible to a wide audience; They can take many forms, including logic grids, number sequences, and geometry puzzles. The goal is not just to find the correct answer but to enjoy the process of reasoning and discovery. Mathematical puzzles are widely used in education to make learning math enjoyable and to encourage critical thinking. They also serve as a bridge between recreational activities and academic development, appealing to both students and enthusiasts of recreational mathematics.
1.2 Importance of Puzzles in Learning Math
Mathematical puzzles play a vital role in enhancing learning and understanding of mathematics. They provide an interactive and engaging way to develop problem-solving skills, fostering critical thinking and creativity. By presenting challenges in a fun and accessible manner, puzzles help learners build confidence in their mathematical abilities. They also promote cognitive development by encouraging logical reasoning, pattern recognition, and analytical thinking. Unlike traditional math problems, puzzles often require innovative approaches, which can deepen understanding of key concepts. Additionally, puzzles cater to different learning styles, making math more inclusive and enjoyable for diverse audiences. Regular engagement with mathematical puzzles can improve mental agility, persistence, and the ability to tackle complex problems. This makes them a valuable tool for both educational and recreational purposes, bridging the gap between learning and entertainment while fostering a lifelong appreciation for mathematics.

Historical Background
Mathematical puzzles have a rich history, dating back to ancient civilizations, where they were used for both recreational purposes and to shape mathematical thought. They have inspired influential mathematicians and continue to evolve today.
2.1 Evolution of Math Puzzles
Math puzzles have evolved significantly over centuries, reflecting advancements in mathematics and changing societal interests. Ancient civilizations, such as Egyptians and Babylonians, used arithmetic and geometric problems to train scribes and solve practical challenges. These early puzzles were often rooted in real-world applications, like measuring land or calculating resources.
In the Middle Ages, mathematical puzzles became popular as recreational activities among scholars. The Renaissance period saw the rise of algebraic puzzles, while the 19th and 20th centuries introduced iconic puzzles like Sudoku and logic grids. Today, math puzzles are widely available in books, online platforms, and educational resources, catering to diverse skill levels and interests. This evolution highlights the enduring appeal of mathematical puzzles as tools for learning and entertainment.
2.2 Influential Mathematicians and Their Puzzles
Many renowned mathematicians have contributed to the world of puzzles, blending intellectual curiosity with entertainment. Martin Gardner, a pioneer of recreational mathematics, popularized puzzles through his column in Scientific American. His work introduced iconic challenges like the “24 Game,” which requires using all four numbers 1-10 with basic operations to reach 24; Another influential figure is Leonhard Euler, whose “Knight’s Tour” puzzle remains a classic in combinatorial mathematics. Similarly, mathematicians like Henry Dudeney and Sam Loyd crafted puzzles that tested logic and spatial reasoning. Their creations, such as Dudeney’s “Haberdasher’s Puzzle” and Loyd’s “Famous 15-Puzzle,” continue to inspire problem solvers. These mathematicians not only advanced mathematical thinking but also made puzzles accessible and engaging for a broader audience, leaving a lasting legacy in recreational mathematics.

Types of Mathematical Puzzles
Mathematical puzzles come in diverse forms, including logic grids, number sequences, and geometry challenges. Each type stimulates different cognitive skills, enhancing problem-solving abilities and logical reasoning.
3.1 Logic Grids
Logic grids are a popular type of mathematical puzzle that require deductive reasoning and systematic analysis. These puzzles typically present a scenario with various elements, such as people, places, or objects, and provide clues to determine the correct arrangement or assignment. Solving logic grids involves creating a table or grid to organize the information and eliminate possibilities through logical deductions. They are often found in puzzle books and online resources, offering a challenging yet rewarding experience for enthusiasts; Logic grids enhance critical thinking, attention to detail, and the ability to break down complex problems into manageable steps. They are particularly effective for developing analytical skills and are enjoyed by both casual puzzlers and competitive solvers alike.
3.2 Number Sequences
Number sequences are classic mathematical puzzles that test pattern recognition and numerical reasoning. These puzzles present a series of numbers with a hidden rule or relationship, and the challenge is to identify the next number or complete the sequence. They can involve arithmetic progressions, geometric patterns, or more complex logical connections. For example, a sequence like 2, 4, 8, 16 requires recognizing the doubling pattern to determine the next number, which is 32. Number sequences are widely featured in puzzle books and online resources, making them accessible to a broad audience. Solving these puzzles enhances mathematical intuition, problem-solving abilities, and the capacity to think logically. They are particularly useful for improving cognitive skills and are enjoyed by both students and experienced puzzle enthusiasts as a fun and engaging mental exercise.
3.3 Geometry Puzzles
Geometry puzzles are engaging challenges that involve spatial reasoning, shape manipulation, and visual problem-solving. These puzzles often require identifying patterns, calculating areas, or reconstructing shapes. Examples include tangram puzzles, where players arrange triangles to form specific figures, and Sudoku, which combines geometry with numerical logic. Geometry puzzles enhance spatial awareness, critical thinking, and mathematical comprehension. They are particularly effective for developing visual-spatial skills and fostering creativity. Many geometry puzzles are featured in mathematical puzzle books and online resources, offering a variety of difficulty levels. Solving these puzzles helps learners understand geometric principles in an interactive and enjoyable way. Additionally, geometry puzzles often overlap with art and design, making them appealing to a diverse audience. They are a popular choice for both educational and recreational purposes, providing a unique blend of challenge and intellectual stimulation.

Educational Benefits
Mathematical puzzles enhance cognitive abilities, improve problem-solving skills, and foster critical thinking, making them valuable tools for educational development and intellectual growth in students of all ages.
4.1 Cognitive Development Through Puzzles
Mathematical puzzles play a significant role in enhancing cognitive development by improving problem-solving skills and logical reasoning. They stimulate the brain, fostering critical thinking and creativity. Engaging with puzzles strengthens spatial awareness and numerical understanding, essential for grasping advanced mathematical concepts. Additionally, they enhance memory and attention, as solving puzzles requires focus and mental discipline. The structured nature of puzzles helps individuals develop analytical thinking, breaking down complex problems into manageable steps. Over time, regular puzzle-solving can boost confidence and academic performance, particularly in mathematics. Moreover, puzzles cater to different learning styles, making them an inclusive tool for cognitive growth. By incorporating puzzles into education, students develop a deeper appreciation for mathematics and improved intellectual abilities. This makes puzzles a valuable resource for both educational and personal development, promoting lifelong learning and intellectual curiosity. Their impact on cognitive development is undeniable, making them a timeless educational asset.
4.2 Enhancing Problem-Solving Skills
Mathematical puzzles are a powerful tool for enhancing problem-solving skills, encouraging individuals to approach challenges methodically and creatively. They help people develop systematic thinking, breaking down complex problems into simpler, manageable parts. Regular engagement with puzzles improves analytical reasoning, teaching individuals to evaluate information, identify patterns, and draw logical conclusions. These skills are transferable to various aspects of life, including academics and real-world scenarios. Puzzles also foster resilience, as they often require persistence and adaptability to find solutions. By practicing with different types of puzzles, such as logic grids and number sequences, individuals can refine their critical thinking abilities. This enhances their capacity to tackle a wide range of mathematical and non-mathematical problems with confidence and efficiency. Ultimately, mathematical puzzles serve as an effective means of sharpening problem-solving skills, making them an invaluable educational resource for learners of all ages. They promote intellectual growth and practical application of mathematical concepts.

Resources for Mathematical Puzzles
Mathematical puzzles are widely available in PDF books and online collections, offering diverse challenges for learners. Websites and publications provide endless fun and educational resources for puzzle enthusiasts.
5.1 Recommended PDF Books
For enthusiasts seeking comprehensive collections, several PDF books stand out. Titles like “The Scientific American Book of Mathematical Puzzles and Diversions” offer a wide array of challenges, blending classic and modern problems. These books are designed to cater to both beginners and advanced puzzle solvers, providing insights into higher levels of mathematical thinking. Many PDF resources are available online, such as the “Math Puzzles for Grade 6” booklet, which simplifies concepts for younger learners. Additionally, compilations like “300 of the World’s Best Mathematical Puzzles” are perfect for those looking to test their skills extensively. These PDF books are not only educational but also entertaining, making them ideal for anyone interested in recreational mathematics.
5.2 Websites Offering Puzzle Collections
Several websites provide extensive collections of mathematical puzzles in PDF format, catering to diverse skill levels and interests. Platforms like Math Puzzlers offer a variety of activities designed to make learning mathematics enjoyable. Educational websites often feature downloadable resources, such as the “Math Puzzles for Grade 6” booklet, which simplifies complex concepts for younger audiences. Additionally, sites dedicated to recreational mathematics curate puzzles that challenge problem-solving skills and foster creative thinking. These online resources are invaluable for both students and enthusiasts, providing accessible and engaging ways to explore mathematical puzzles. By leveraging these websites, users can easily find and download PDF materials tailored to their learning needs, making them a great supplement to traditional educational tools.

Solving Strategies
Effective strategies for solving mathematical puzzles involve systematic approaches, such as breaking down problems into smaller parts or identifying patterns. Logical reasoning and creative thinking are essential tools.
6.1 Approaches to Tackling Different Puzzle Types
Different mathematical puzzles require tailored strategies. For logic grids, creating tables to track possibilities is effective. Number sequences often involve identifying patterns or arithmetic progressions. Geometry puzzles benefit from visualizing shapes and using spatial reasoning. Breaking problems into smaller, manageable parts is a universal approach. Practicing with various puzzle types enhances adaptability and sharpens analytical skills. Starting with simpler puzzles builds confidence before tackling more complex ones. Using elimination techniques and reverse engineering solutions are also valuable methods. Combining creativity with systematic thinking often leads to breakthroughs. Regular practice helps develop intuition and improves problem-solving efficiency over time. These strategies foster a deeper understanding of mathematical concepts while making puzzle-solving an enjoyable and rewarding experience.
6.2 Common Mistakes to Avoid
When solving mathematical puzzles, several common mistakes can hinder progress. Rushing through problems without understanding the rules is a frequent error, leading to incorrect assumptions. Overlooking simple patterns or misinterpreting clues is another pitfall. Jumping to conclusions without verifying each step can result in wrong answers. Neglecting to check work increases the likelihood of errors. Overcomplicating puzzles by introducing unnecessary steps is also a mistake. Failing to break problems into smaller parts can make them appear insurmountable. Ignoring the importance of careful reading and attention to detail is a common oversight. Avoiding these mistakes requires patience, thoroughness, and a systematic approach. By learning from these errors, puzzlers can improve their skills and enjoy a more rewarding experience. Practicing mindfulness and staying methodical are key to avoiding these traps and solving puzzles effectively.

Popular Mathematical Puzzles
Mathematical puzzles like the 24 Game and Sudoku are widely recognized for their challenging yet engaging nature. These puzzles test arithmetic, logic, and problem-solving skills, fostering mental agility and strategic thinking.
7.1 The Famous 24 Game
The 24 Game is a timeless mathematical puzzle that challenges players to use four numbers, each exactly once, with basic arithmetic operations to reach the total of 24. This game, often played with cards, has been a favorite among math enthusiasts since its creation in the 1960s. It requires a combination of creativity, quick thinking, and a solid understanding of arithmetic principles. The game’s simplicity belies its depth, making it accessible to both children and adults. The 24 Game has inspired numerous variations and competitions, cementing its place as a classic in the world of mathematical puzzles.
7.2 Sudoku and Its Variants
Sudoku is a cornerstone of mathematical puzzles, offering a number-based challenge that requires logic and reasoning. Originating in Japan, Sudoku presents a 9×9 grid divided into nine 3×3 subgrids, with some numbers pre-filled. The goal is to fill in the remaining cells so that each row, column, and subgrid contains all numbers from 1 to 9 without repetition. Its popularity lies in its ability to enhance cognitive skills while providing an enjoyable mental workout. Over time, various Sudoku variants have emerged, such as Mini Sudoku (4×4 grid), Jigsaw Sudoku (irregular shapes), and Hyper Sudoku (additional constraints). These variations keep the puzzle fresh and cater to different skill levels. Sudoku’s global appeal has made it a staple in recreational mathematics, with numerous PDF resources available for enthusiasts to explore its diverse forms and challenges.

Cultural and Competitive Impact
Mathematical puzzles reflect diverse cultural problem-solving styles, fostering global interest and community. They inspire competitions, celebrating intellectual achievements and creativity, while bridging cultural gaps through shared enthusiasm for logical challenges.
8.1 Puzzles in Different Cultures
Mathematical puzzles are a universal form of intellectual entertainment, appearing in diverse cultures worldwide. From ancient civilizations to modern times, each culture has developed unique puzzle traditions that reflect their mathematical understanding and problem-solving methods. For example, Japanese Sudoku combines logic and number patterns, while African puzzles often incorporate geometric shapes and spatial reasoning. In India, puzzles like the “24 Game” and Vedic mathematics have been popular for centuries, emphasizing mental calculation and arithmetic skills. Similarly, European cultures have contributed puzzles such as logic grids and algebraic riddles. These puzzles not only entertain but also provide insights into the mathematical knowledge and values of different societies, making them a fascinating subject of study and appreciation.
8.2 Competitive Events and Puzzle Championships
Competitive events and puzzle championships have become a significant part of the mathematical puzzle community. These events bring together enthusiasts from around the globe to test their problem-solving skills and strategic thinking. The World Puzzle Championship, for instance, is an annual event where participants solve a variety of mathematical and logic-based puzzles under time constraints. Similarly, the International Mathematical Olympiad (IMO) challenges students with advanced mathematical problems, fostering a competitive yet collaborative environment. These competitions not only highlight individual brilliance but also promote the development of new puzzle types and strategies. They serve as platforms for innovation and learning, inspiring participants to push the boundaries of mathematical creativity. As a result, competitive puzzle events continue to grow in popularity, attracting a diverse range of participants and spectators alike.
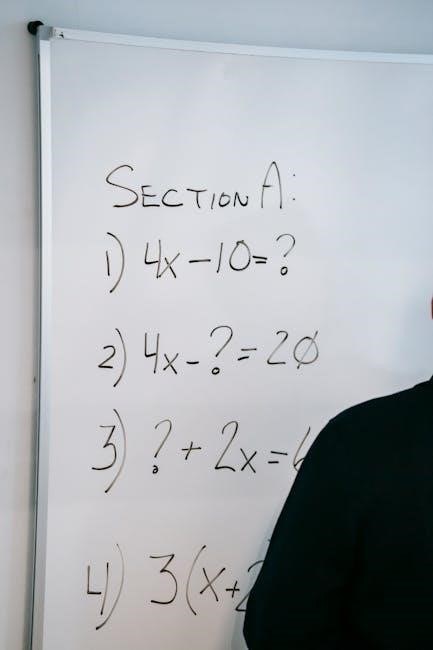
Advanced Puzzles for Enthusiasts
Advanced mathematical puzzles challenge enthusiasts with complex problems involving higher-level mathematics. These puzzles, often found in dedicated PDF books, cater to those seeking intellectual stimulation and mastery of numerical logic.
9.1 Puzzles Involving Higher Mathematics
Puzzles involving higher mathematics challenge enthusiasts with complex concepts like algebra, calculus, and number theory. These puzzles, often featured in specialized PDF books, require advanced problem-solving skills and deep mathematical knowledge. They cater to individuals passionate about exploring intricate numerical relationships and logical reasoning. Many of these puzzles have historical roots, inspired by influential mathematicians who used recreational math to illustrate profound ideas. For example, puzzles involving infinite series or modular arithmetic can be both intellectually stimulating and aesthetically rewarding. Solving such puzzles enhances analytical thinking and fosters a deeper appreciation for mathematical principles. Enthusiasts often seek out these challenges in dedicated resources, where they can engage with like-minded individuals and push their cognitive limits. Such puzzles are not just games but gateways to understanding higher-level mathematics in a fun and engaging way.
9.2 Historical Puzzles and Their Significance

Historical mathematical puzzles offer a glimpse into the evolution of mathematical thought and cultural traditions. Many classic puzzles, such as the 24 Game and Sudoku, have origins tied to specific eras and regions, reflecting the intellectual curiosity of their times. These puzzles often emerged as tools for teaching mathematical concepts or as entertainment for scholars. Influential mathematicians like Fibonacci and Euler contributed to the development of recreational math, blending logic with creativity. Historical puzzles not only showcase mathematical ingenuity but also highlight how different cultures approached problem-solving. Their significance lies in their ability to inspire learning and critical thinking while preserving mathematical history. Today, these puzzles are widely available in PDF collections, allowing modern enthusiasts to connect with the past and appreciate the timeless appeal of mathematical challenges.
Mathematical puzzles continue to grow in popularity, with digital platforms and PDF resources making them more accessible. Future trends include interactive puzzles and AI-driven challenges, enhancing learning and fun.
10.1 The Growing Popularity of Math Puzzles
Math puzzles have seen a significant rise in popularity due to their universal appeal and accessibility. PDF resources and online platforms have made them widely available, catering to diverse skill levels and interests. These puzzles not only entertain but also serve as valuable educational tools, fostering problem-solving and critical thinking. Their ability to combine fun with learning has attracted both students and professionals, making them a staple in modern educational curricula. Additionally, cultural exchange has highlighted the global appreciation for mathematical puzzles, further fueling their growth. As technology evolves, interactive and dynamic puzzles are emerging, ensuring their continued relevance. The blend of intellectual challenge and enjoyment makes math puzzles a beloved and enduring activity worldwide.
10.2 Innovations in Puzzle Creation and Distribution
Modern advancements in technology have revolutionized the creation and distribution of mathematical puzzles. PDF books and online platforms now offer interactive puzzles, enabling users to solve them digitally. AI algorithms generate puzzles tailored to individual skill levels, enhancing personalization. Virtual reality (VR) and augmented reality (AR) are being explored to create immersive puzzle experiences. Social media and online communities facilitate sharing and collaboration, fostering a global puzzle-solving culture. Mobile apps deliver puzzles directly to users, making them accessible anytime, anywhere. These innovations ensure that mathematical puzzles remain engaging and relevant in the digital age, attracting a broader audience and keeping the tradition alive for future generations.

